跳至主要內容

图

2025/8/26数据结构与算法图

图

图

图（graph）是一种非线性数据结构，由顶点（vertex）和边（edge）组成。

常见类型和术语

图的分类：

  • 根据边是否具有方向：
    • 有向图
    • 无向图
  • 根据所有定点是否连通：
    • 连通图：从某个顶点出发，可以到达其余任意顶点
    • 非连通图：从某个顶点出发，至少有一个顶点无法到达
  • 边是否有权重：
    • 无权图
    • 有权图

图的常用术语：

  • 邻接：当两顶点之间存在边相连时，称这两顶点“邻接”。
  • 路径：从顶点 A 到顶点 B 经过的边构成的序列被称为从 A 到 B 的“路径”。
  • 度：一个顶点拥有的边数。对于有向图，入度表示有多少条边指向该顶点，出度表示有多少条边从该顶点指出。

图的表示

邻接矩阵

设图的顶点数量为 n，邻接矩阵使用一个 n×n 大小的矩阵来表示图，每一行（列）代表一个顶点，矩阵元素代表边，用 1 或 0 表示两个顶点之间是否存在边。
设邻接矩阵为 M、顶点列表为 V，那么矩阵元素 M[i,j]=1 表示顶点 V[i] 到顶点 V[j] 之间存在边，反之 M[i,j]=0 表示两顶点之间无边。

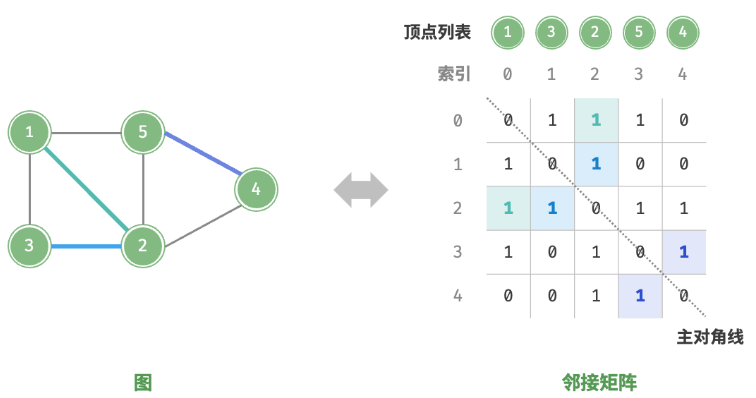
alt text
alt text

邻接矩阵具有以下特性。

  • 在简单图中，顶点不能与自身相连，此时邻接矩阵主对角线元素没有意义。
  • 对于无向图，两个方向的边等价，此时邻接矩阵关于主对角线对称。
  • 将邻接矩阵的元素从1和0替换为权重，则可表示有权图。

使用邻接矩阵表示图时，可以直接访问矩阵元素以获取边，因此增删查改操作的效率很高，时间复杂度均为 O(1)。然而，矩阵的空间复杂度为O(n2)，内存占用较多。

邻接表

邻接表使用 n 个链表来表示图，链表节点表示顶点。第i个链表对应顶点i ，其中存储了该顶点的所有邻接顶点。

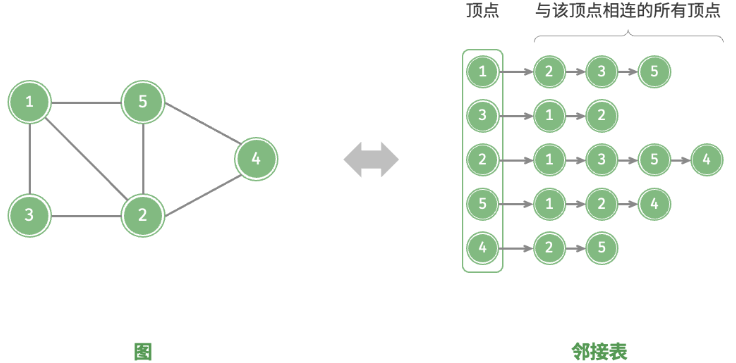
alt text
alt text

邻接表仅存储实际存在的边，而边的总数通常远小于 n2，因此它更加节省空间。然而，在邻接表中需要通过遍历链表来查找边，因此其时间效率不如邻接矩阵。

邻接表结构与哈希表中的 “链式地址” 非常相似，因此也可以采用类似的方法来优化效率。当链表较长时，可以将链表转化为 AVL 树或红黑树，从而将时间效率从 O(n) 优化至 O(log⁡n)；还可以把链表转换为哈希表，从而将时间复杂度降至 O(1)。

图的基础操作

基于邻接矩阵的实现

  • 添加或删除边：直接在邻接矩阵中修改指定的边即可，使用 O(1) 时间。而由于是无向图，因此需要同时更新两个方向的边。
  • 添加顶点：在邻接矩阵的尾部添加一行一列，并全部填 0 即可，使用 O(n) 时间。
  • 删除顶点：在邻接矩阵中删除一行一列。当删除首行首列时达到最差情况，需要将 (n−1)2 个元素 “向左上移动”，从而使用 O(n2) 时间。
  • 初始化：传入 n 个顶点，初始化长度为 n 的顶点列表 vertices ，使用 O(n) 时间；初始化 n×n 大小的邻接矩阵 adjMat ，使用 O(n2) 时间。
/* 基于邻接矩阵实现的无向图类 */
class GraphAdjMat {
    List<Integer> vertices; // 顶点列表，元素代表“顶点值”，索引代表“顶点索引”
    List<List<Integer>> adjMat; // 邻接矩阵，行列索引对应“顶点索引”

    /* 构造方法 */
    public GraphAdjMat(int[] vertices, int[][] edges) {
        this.vertices = new ArrayList<>();
        this.adjMat = new ArrayList<>();
        // 添加顶点
        for (int val : vertices) {
            addVertex(val);
        }
        // 添加边
        // 请注意，edges 元素代表顶点索引，即对应 vertices 元素索引
        for (int[] e : edges) {
            addEdge(e[0], e[1]);
        }
    }

    /* 获取顶点数量 */
    public int size() {
        return vertices.size();
    }

    /* 添加顶点 */
    public void addVertex(int val) {
        int n = size();
        // 向顶点列表中添加新顶点的值
        vertices.add(val);
        // 在邻接矩阵中添加一行
        List<Integer> newRow = new ArrayList<>(n);
        for (int j = 0; j < n; j++) {
            newRow.add(0);
        }
        adjMat.add(newRow);
        // 在邻接矩阵中添加一列
        for (List<Integer> row : adjMat) {
            row.add(0);
        }
    }

    /* 删除顶点 */
    public void removeVertex(int index) {
        if (index >= size())
            throw new IndexOutOfBoundsException();
        // 在顶点列表中移除索引 index 的顶点
        vertices.remove(index);
        // 在邻接矩阵中删除索引 index 的行
        adjMat.remove(index);
        // 在邻接矩阵中删除索引 index 的列
        for (List<Integer> row : adjMat) {
            row.remove(index);
        }
    }

    /* 添加边 */
    // 参数 i, j 对应 vertices 元素索引
    public void addEdge(int i, int j) {
        // 索引越界与相等处理
        if (i < 0 || j < 0 || i >= size() || j >= size() || i == j)
            throw new IndexOutOfBoundsException();
        // 在无向图中，邻接矩阵关于主对角线对称，即满足 (i, j) == (j, i)
        adjMat.get(i).set(j, 1);
        adjMat.get(j).set(i, 1);
    }

    /* 删除边 */
    // 参数 i, j 对应 vertices 元素索引
    public void removeEdge(int i, int j) {
        // 索引越界与相等处理
        if (i < 0 || j < 0 || i >= size() || j >= size() || i == j)
            throw new IndexOutOfBoundsException();
        adjMat.get(i).set(j, 0);
        adjMat.get(j).set(i, 0);
    }

    /* 打印邻接矩阵 */
    public void print() {
        System.out.print("顶点列表 = ");
        System.out.println(vertices);
        System.out.println("邻接矩阵 =");
        PrintUtil.printMatrix(adjMat);
    }
}

基于邻接表的实现

点数n，边数m的无向图：

  • 添加边：在顶点对应链表的末尾添加边即可，使用 O(1) 时间。因为是无向图，所以需要同时添加两个方向的边。
  • 删除边：在顶点对应链表中查找并删除指定边，使用 $O(m) $ 时间。在无向图中，需要同时删除两个方向的边。
  • 添加顶点：在邻接表中添加一个链表，并将新增顶点作为链表头节点，使用 O(1) 时间。
  • 删除顶点：需遍历整个邻接表，删除包含指定顶点的所有边，使用 O(n+m) 时间。
  • 初始化：在邻接表中创建 n 个顶点和 2m 条边，使用 O(n+m) 时间。
/* 基于邻接表实现的无向图类 */
class GraphAdjList {
    // 邻接表，key：顶点，value：该顶点的所有邻接顶点
    // 这里采用List代替链表，并采用hash表来存储
    // Vertex类表示顶点
    Map<Vertex, List<Vertex>> adjList;

    /* 构造方法 */
    public GraphAdjList(Vertex[][] edges) {
        this.adjList = new HashMap<>();
        // 添加所有顶点和边
        for (Vertex[] edge : edges) {
            addVertex(edge[0]);
            addVertex(edge[1]);
            addEdge(edge[0], edge[1]);
        }
    }

    /* 获取顶点数量 */
    public int size() {
        return adjList.size();
    }

    /* 添加边 */
    public void addEdge(Vertex vet1, Vertex vet2) {
        if (!adjList.containsKey(vet1) || !adjList.containsKey(vet2) || vet1 == vet2)
            throw new IllegalArgumentException();
        // 添加边 vet1 - vet2
        adjList.get(vet1).add(vet2);
        adjList.get(vet2).add(vet1);
    }

    /* 删除边 */
    public void removeEdge(Vertex vet1, Vertex vet2) {
        if (!adjList.containsKey(vet1) || !adjList.containsKey(vet2) || vet1 == vet2)
            throw new IllegalArgumentException();
        // 删除边 vet1 - vet2
        adjList.get(vet1).remove(vet2);
        adjList.get(vet2).remove(vet1);
    }

    /* 添加顶点 */
    public void addVertex(Vertex vet) {
        if (adjList.containsKey(vet))
            return;
        // 在邻接表中添加一个新链表
        adjList.put(vet, new ArrayList<>());
    }

    /* 删除顶点 */
    public void removeVertex(Vertex vet) {
        if (!adjList.containsKey(vet))
            throw new IllegalArgumentException();
        // 在邻接表中删除顶点 vet 对应的链表
        adjList.remove(vet);
        // 遍历其他顶点的链表，删除所有包含 vet 的边
        for (List<Vertex> list : adjList.values()) {
            list.remove(vet);
        }
    }

    /* 打印邻接表 */
    public void print() {
        System.out.println("邻接表 =");
        for (Map.Entry<Vertex, List<Vertex>> pair : adjList.entrySet()) {
            List<Integer> tmp = new ArrayList<>();
            for (Vertex vertex : pair.getValue())
                tmp.add(vertex.val);
            System.out.println(pair.getKey().val + ": " + tmp + ",");
        }
    }
}

效率对比

定点数n，边树数m的图：

邻接矩阵邻接表（链表）邻接表（哈希表）
判断是否邻接O(1)O(n)O(1)
添加边O(1)O(1)O(1)
删除边O(1)O(n)O(1)
添加顶点O(n)O(1)O(1)
删除顶点O(n2)O(n+m)O(n)
内存空间占用O(n2)O(n+m)O(n+m)

这里添加顶点，就只考虑添加顶点，添加顶点的同时还会有边的添加，那属于添加边。

图的遍历

树代表的是“一对多”的关系，而图可以表示任意的“多对多”关系。因此，可以把树看作图的一种特例，树的遍历操作也是图的遍历操作的一种特例。

图和树都需要应用搜索算法来实现遍历操作。图的遍历方式也可分为两种：广度优先遍历和深度优先遍历。

广搜BFS

通常借助队列来实现

  1. 将遍历起始顶点 startVet 加入队列，并开启循环。
  2. 在循环的每轮迭代中，弹出队首顶点并记录访问，然后将该顶点的所有邻接顶点加入到队列尾部。
  3. 循环步骤 2. ，直到所有顶点被访问完毕后结束。

借助一个哈希集合 visited 来记录哪些节点已被访问。

时间复杂度：所有顶点都会入队并出队一次，使用 O(|V|) 时间；在遍历邻接顶点的过程中，由于是无向图，因此所有边都会被访问 2 次，使用 O(2|E|) 时间；总体使用 O(|V|+|E|) 时间。

空间复杂度：列表 res，哈希集合 visited，队列 que 中的顶点数量最多为 |V|，使用 O(|V|) 空间。

/* 广度优先遍历 */
// 使用邻接表来表示图，以便获取指定顶点的所有邻接顶点
List<Vertex> graphBFS(GraphAdjList graph, Vertex startVet) {
    // 顶点遍历序列
    List<Vertex> res = new ArrayList<>();
    // 哈希集合，用于记录已被访问过的顶点
    Set<Vertex> visited = new HashSet<>();
    visited.add(startVet);
    // 队列用于实现 BFS
    Queue<Vertex> que = new LinkedList<>();
    que.offer(startVet);
    // 以顶点 vet 为起点，循环直至访问完所有顶点
    while (!que.isEmpty()) {
        Vertex vet = que.poll(); // 队首顶点出队
        res.add(vet);            // 记录访问顶点
        // 遍历该顶点的所有邻接顶点
        for (Vertex adjVet : graph.adjList.get(vet)) {
            if (visited.contains(adjVet))
                continue;        // 跳过已被访问的顶点
            que.offer(adjVet);   // 只入队未访问的顶点
            visited.add(adjVet); // 标记该顶点已被访问
        }
    }
    // 返回顶点遍历序列
    return res;
}

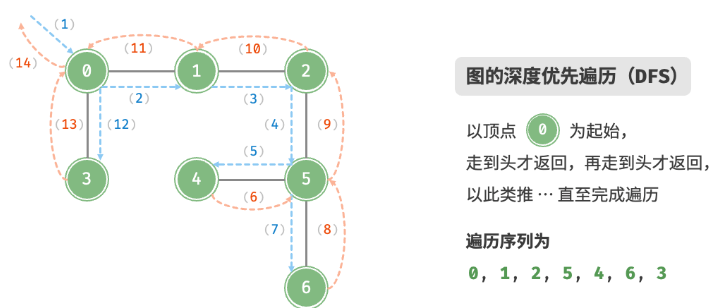
深搜DFS

时间复杂度：所有顶点都会被访问 1 次，使用 O(|V|) 时间；所有边都会被访问 2 次，使用 O(2|E|) 时间；总体使用 O(|V|+|E|) 时间。

空间复杂度：列表 res，哈希集合 visited 顶点数量最多为 |V|，递归深度最大为 |V|，因此使用 O(|V|) 空间。

alt text
alt text
/* 深度优先遍历函数 */
void dfs(GraphAdjList graph, Set<Vertex> visited, List<Vertex> res, Vertex vet) {
    res.add(vet);     // 记录访问顶点
    visited.add(vet); // 标记该顶点已被访问
    // 遍历该顶点的所有邻接顶点
    for (Vertex adjVet : graph.adjList.get(vet)) {
        if (visited.contains(adjVet))
            continue; // 跳过已被访问的顶点
        // 递归访问邻接顶点
        dfs(graph, visited, res, adjVet);
    }
}

/* 深度优先遍历 */
// 使用邻接表来表示图，以便获取指定顶点的所有邻接顶点
List<Vertex> graphDFS(GraphAdjList graph, Vertex startVet) {
    // 顶点遍历序列
    List<Vertex> res = new ArrayList<>();
    // 哈希集合，用于记录已被访问过的顶点
    Set<Vertex> visited = new HashSet<>();
    dfs(graph, visited, res, startVet);
    return res;
}

树的前中后序遍历都属于深搜